Nous avons exploré dans les deux derniers articles le principe de la lecture d’échantillons. Cela nous a permis, entre autres, de constater que, grâce au numérique, les frontières entre les différents modes de génération du son – par exemple entre ondes simples et échantillons complexes pré-enregistrés — devenaient de plus en plus poreuses.
La synthèse granulaire, sur laquelle nous allons nous concentrer aujourd’hui, est une illustration supplémentaire de cette convergence. Elle est basée sur une nouvelle unité de base sonore, que nous avons déjà brièvement évoquée dans l’article 4 de cette série : le grain.
Mais commençons par…
Un tout petit peu d’histoire
Sans entrer dans des détails qui n’auraient pas leur place ici, sachez que la synthèse granulaire a été pour la première fois évoquée de manière théorique en 1925 par Norbert Wiener. C’est lui qui a eu le premier l’idée d’appliquer à la musique la notion des « grains d’énergie » de la physique quantique.
Mais c’est le prix Nobel de physique et inventeur de l’hologramme Dennis Gabor (voir paragraphe suivant) qui l’a théorisée en 1947 avant d’être totalement validée par Martin Bastiaans en 1980. Ce qui n’a pas empêché Curtis Roads, dès 1978, d’en implémenter des éléments pour la première fois de manière logicielle.
Iannis Xenakis (voir photo) et le compositeur chercheur Barry Truax sont les principaux ambassadeurs artistiques de ce type de synthèse.
Gabor et les limites de la théorie de Fourier
Gabor est parti de la constatation que la théorie de Fourier, si elle est parfaite pour déterminer les composantes harmoniques d’un signal sonore, n’est par contre pas capable de déterminer la localisation temporelle de ces dernières. En conséquence, elle n’est pas adaptée à l’analyse et à la resynthèse d’un signal évoluant dans le temps.
Pour simplifier la chose pour les musiciens que nous sommes, on peut dire par exemple qu’elle sera incapable de différencier un accord (un certain nombre de notes jouées simultanément) et l’arpège de celui-ci (les mêmes notes jouées consécutivement). Cela est dû, entre autres, au fait que la théorie de Fourier réduit le signal à des sinusoïdes simples… de durée infinie. Il fallait donc trouver d’autres éléments de base que ces dernières si l’on voulait synthétiser des sons évolutifs. Les grains sont la concrétisation de cette recherche.
Les grains au microscope
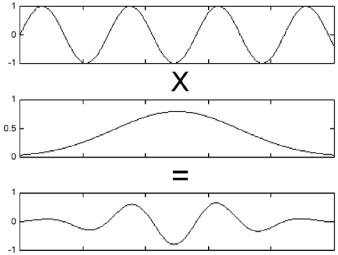
En effet, les grains présentent un avantage énorme par rapport aux sinusoïdes de Fourier : ils sont délimités dans le temps ! Ils disposent à la fois d’un point de départ et d’une enveloppe modulante (voir article 8 de cette série) qui englobe la forme d’onde elle-même.
Ci-contre, l’illustration d’une sinusoïde soumise à une enveloppe. Cette forme d’onde peut être une forme d’onde simple, ou bien par exemple un signal issu d’autres types de synthèse, par exemple la modulation de fréquence (synthèse FM) que nous étudierons très prochainement. La forme d’onde peut en outre avoir été stockée dans une table d’ondes (voir article précédent). Ou encore, il peut s’agir d’un élément tiré d’un signal sonore complexe tel que la numérisation d’une note de musique jouée par un instrument.
Chaque grain comporte également ses propres informations de fréquences — définissant sa hauteur — et de phase. La longueur du grain va déterminer notre capacité à percevoir la hauteur de ce dernier. En effet, il a été prouvé qu’en dessous de 100 ms, l’oreille humaine n’est plus en mesure d’évaluer la hauteur et le contenu spectral (harmonique) d’un grain. À noter que plus le grain sera court, et plus il sera aisé de le situer temporellement, et plus il sera long, plus ce sera son contenu harmonique qu’il sera facile d’identifier.
La longueur du grain, ainsi que l’amplitude de sa forme d’onde, est définie par son enveloppe. Celle-ci peut être à segments (attack, « steady state » équivalent au « sustain » des enveloppes traditionnelles, et release) ou « fonctionnelle », c’est-à-dire basée sur une fonction mathématique. Elle peut être elle-même sauvegardée dans une table d’ondes — ou plutôt une « table d’enveloppes » dans ce cas précis — avec les mêmes avantages que concernant les échantillons (voir article précédent).
L’enveloppe peut être également affublée d’un paramètre de gestion du panoramique, permettant de localiser les grains dans l’espace.
Lecture des grains
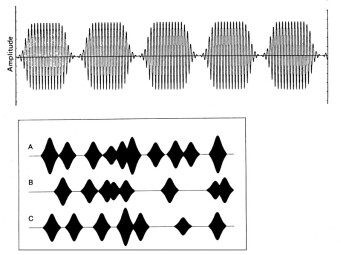
Il ne s’agit plus forcément de lire les grains consécutivement comme lors de la lecture d’échantillons « première définition » (voir article précédent). Nous verrons dans le prochain article qu’il existe différentes manières de lire les grains, chacune faisant l’objet d’une sous-catégorie de la synthèse granulaire. Toutefois, on peut dire que dans tous les cas de figure, la lecture est soumise à un paramètre d’espacement entre les grains. Ce dernier peut être représenté par une fréquence ou bien un temps fixe (période).
Dans le cas de l’utilisation d’une fréquence, plus celle-ci est basse, et plus l’effet ressenti sera celui d’une rythmique, plus elle est haute et plus l’effet sera associé à une hauteur de note.
Ci-contre, des grains sonores regroupés de diverses manières : On observe donc – à la lecture de nos deux derniers paragraphes – que si la hauteur de chaque grain est contenue en lui-même, la perception que nous aurons de la hauteur globale d’un signal sonore composé de grains dépend de deux facteurs : la longueur de ces grains et leur densité (définie par la fréquence de leur déclenchement).